Two types of losses occur in a transformer. We refer to these losses collectively as losses in Transformers. These two losses are no-load losses and copper losses. We also often refer to the no-load losses as core losses. These losses occur due to the magnetic material of the core of the transformer. These losses include both hysteresis loss and eddy current loss. The core flux remains constant at both the no-load condition and the loaded condition. In other words, the core losses more or less remain constant at all loading conditions of the transformer. So, we refer to the core losses as the constant losses of the transformer.
Expressions of Core Losses
We express the Eddy current loss as
\[W_e = K_e f^2 K_f^2 B_m^2 \text{ watts}\] Where
- \(K_e\) is the Eddy current constant,
- f is the frequency,
- \(K_f\) is the form factor, and
- \(B_m\) is the maximum flux density of the core.
Whereas hysteresis loss \[W_h = K_hf B_m^{1.6}\text{ watts}\]
Here \(K_h\) is the hysteresis loss constant.
Cause of Eddy Current Loss
Actually, alternating magnetising current induces a circulating current in the core material. The core material is also conductive. However, the transformer cannot use this current at the output. Rather, it circulates inside the core, through the conducting path of the core. This Eddy current produces heat in the core. This generated heat is nothing but the power loss. Ultimately, the input source of the transformer contributes to this heat loss. Therefore, the Eddy current causes a power loss.
Cause of Hysteresis Loss.
We use cold-rolled grain-oriented silicon, steel, or amorphous core for constructing the transformer core. Due to the alternating current, the magnetic polarity of the core changes in sync with the current’s rhythm. As a result, the grains of the core reorient themselves along the changing axis of the magnetic field. These orientations and reorientations consume electrical power from the source. This is the hysteresis loss.
Load Losses
Now we connect the load with the transformer. Therefore, the load current starts flowing. As a result, there is a significant flow of current in the primary as well as the secondary windings. Obviously, this current produces ohmic loss in the transformer windings.
We also refer to this ohmic loss as copper loss of the transformer. Obviously, this loss is directly proportional to the square of the current taken by the transformer from the source
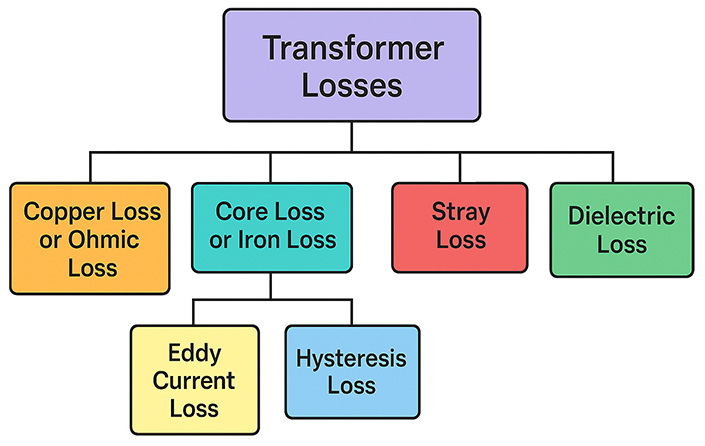
Stray Loss.
The current flowing through the primary creates fluxes. Additionally, the secondary current creates its own flux. Obviously, the secondary flux will neutralise the primary flux inside the core. But what about the leakage fluxes?
The leakage fluxes by both windings remain unaffected by the opposite flux. So, these leakage fluxes can link with the mechanical metal structure and conductors of the transformer. These alternatingly changing leakage fluxes may produce a local, small circulating current in the conducting parts of the transformer. As a result, there will be an additional heat loss in the transformer. This is the stray loss of the transformer.
So, the total loss that we measure during the short-circuit test is the sum of \(I^2R\) loss and stray loss.
Ohmic Loss During Open Circuit Test
We can measure the core loss of a transformer during an open-circuit test. There is also a small quantity of ohmic loss hidden in the total measured core loss during the open-circuit test. This is the ohmic loss due to the flow of only magnetising current through the primary winding. We normally ignore this loss during our calculations. This is because this loss is very, very small compared to the total core loss of the transformer.
Dielectric Loss in a Power Transformer
Dielectric loss occurs in the insulation system of the transformer. It happens when the transformer operates with alternating voltage. The insulation materials include oil, paper, and pressboard. These materials act as dielectrics between live parts. When we apply AC voltage, an electric field develops. The molecules in the dielectric try to align with this field. However, they cannot follow the rapid changes instantly. This delay in polarization causes energy loss as heat. The dielectric loss adds to total transformer losses.
