Kirchhoff’s Current Law and Kirchhoff’s Voltage Law are two very important laws for solving electrical circuit networks. We use these laws mostly to solve network problems.
Kirchhoff’s Current Law
Kirchhoff’s Current Law (KCL) says that the total current entering a node equals the total current leaving the node. Obviously, a node is a point where two or more conductors meet. Actually, the current is nothing but the flow of electrical charge. We know that an electric charge cannot disappear. Also, an electric charge cannot suddenly appear. An electrical charge can only transfer from one point to another in an electric system. This implies the law of conservation of electric charge. So whatever current flows into a node must also flow out of the node.
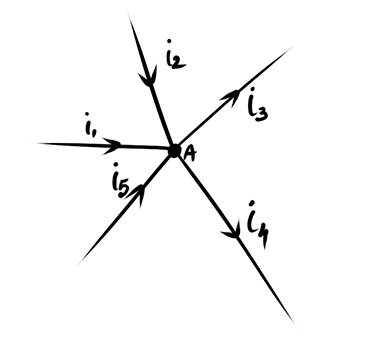
Here, A is the node. As per the diagram, currents i5, i1, and i2 enter the node A at the same instant. At the same instant, currents i3 and i4 leave the same node. Therefore, according to Kirchhoff’s current law, we can write,
We can write this equation (i) as,
Equation (ii) shows that the currents entering the node are positive and the currents leaving the node are negative. So, we can state Kirchhoff’s current law as “the summation of currents entering and leaving a node is always zero”. Therefore, we can write,
Kirchhoff’s Voltage Law
Kirchhoff’s Voltage Law says that around a closed loop of a circuit, the potential gains are equal to the potential drops. If we go through a loop in a certain direction, moving from a lower potential point to a higher potential point implies a voltage (or potential) gain. Conversely, moving from a higher potential point to a lower potential point implies a voltage (or potential) drop. If we consider the voltage gain as positive, then the voltage drop shall be negative. So, by considering the positive and negative signs of voltages (or potentials), we can say that the sum of all voltages around any closed loop in a circuit is zero.
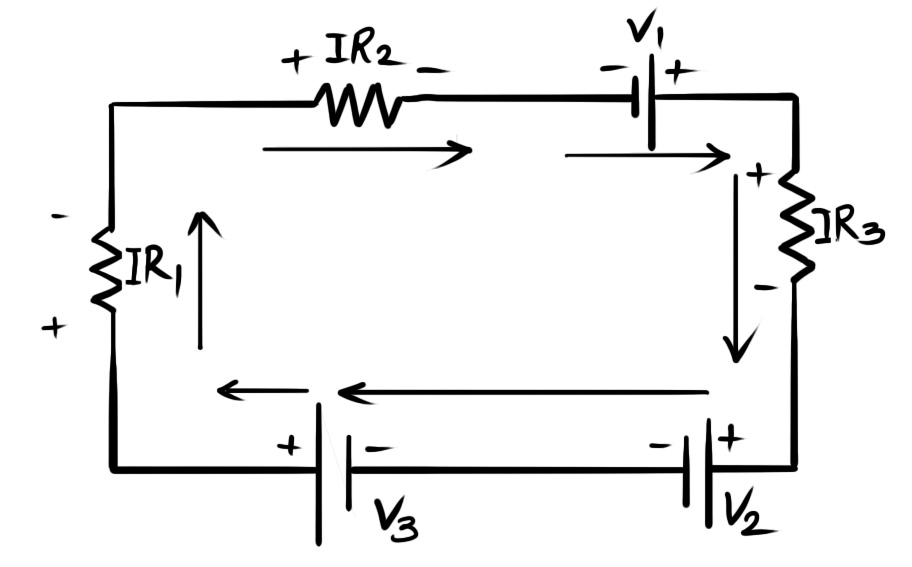
So, we can write as per Kirchhoff’s Voltage Law
Equation (iii) represents the statement of Kirchhoff’s Voltage Law.