What is resistivity? Understand specific resistance, its units (ohm-meter), how material, length, area, and temperature affect conductor resistance.
Laws of Resistance
The resistance offered by a conductor depends upon four major factors.
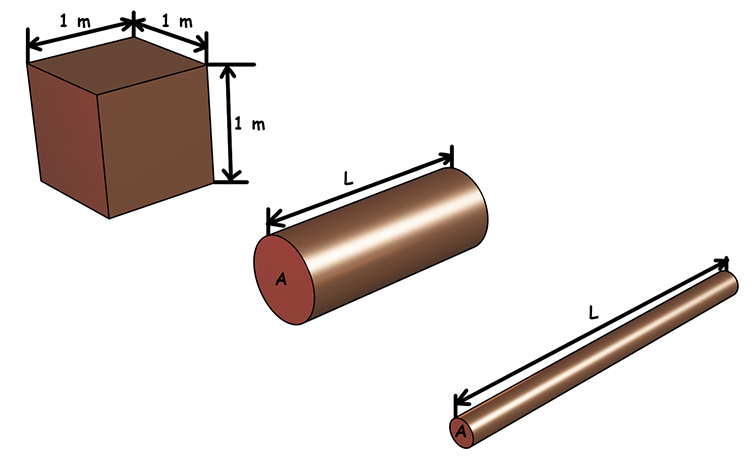
Length of the Conductor: One factor is the length of the conductor. That means if we increase the length of the conductor without changing its cross-sectional area and surrounding temperature, the resistance of the conductor increases linearly with the length. This is because when we lengthen a conductor, each drifting electron has to cover more distance. Therefore, the probability of collisions with other atoms and electrons becomes greater. Mathematically, we can write,\[R \propto L\]Where (L) is the length of the conductor.
Cross-Sectional Area of the Conductor: The resistance of a conductor also varies inversely with the cross-sectional area. This relation is also linear. When the cross-sectional area of a conductor becomes larger, the drifting electrons get a wider space to travel through. Therefore, the obstruction offered by the conductor reduces. Hence, the resistance of the conductor reduces. So mathematically we can write,\[R \propto \frac{1}{A}\]Where (A) is the cross-sectional area of the conductor.
Dependency on the Material and Temperature of the Conductor
Material of the Conductor: Resistance also depends on the material used to construct the conductor. Each conductor has its own ability to conduct current. So the material is another factor that controls the resistance of the conductor.
Metallic Conductors
Temperature: If the temperature increases, atomic vibration in a metallic conductor also increases. So the probability of collision of drifting electrons with atoms becomes greater. Therefore, increased temperature causes an increase in the resistance of the conductor. This is true for metallic conductors.
Semiconductors
In contrast, in semiconductor materials, increased temperature breaks more and more covalent bonds in the crystal structure. These breakdowns of covalent bonds produce more and more free electrons in the semiconductor. Therefore, due to the increased number of electrons in the semiconductor, the current through the semiconductor will increase because more electrons can drift from one point to another point due to the applied electrical field across the semiconductor. So the resistance of the semiconductor decreases with an increase in temperature.
Resistance Formula
Combining these factors, we get,\[R \propto \frac{L}{A}\]\[\Rightarrow R = \rho \frac{L}{A}\]Here \(\rho\) (rho) is the proportionality constant. The value of \(\rho\) depends upon the material used to make the conductor and also depends upon the temperature (which we will discuss later). We refer to this \(\rho\) as the specific resistance or resistivity of the material by which the conductor is made.
Unit of Resistivity
Resistivity is a specific property of a material by which we can predict the capability of carrying current by the conductor for a particular length and cross-section.
Suppose (L) is one meter and (A) is one square meter. Then\[R = \rho\]Hence, the specific resistance of a material is nothing but the resistance offered by a piece of that material whose length is one meter and cross-sectional area is one square meter. If we consider a cube, we can say the resistivity of a specific material is the resistance between two opposite faces of a cube of one cubic meter volume of that material.
Unit Derivation for Specific Resistance
From \(\rho = \frac{RA}{L}\), we can write\[\rho = \frac{A \text{ (m}^2) \times R \text{ (}\Omega\text{)}}{L \text{ (m)}} \]\[= \frac{AR}{L} \text{ }\Omega\text{·m}\]So the unit of resistivity is ohm-meter (\(\Omega\)·m).
If we consider centimeters instead of meters, we can write,\[\rho = \frac{A \text{ (cm}^2) \times R \text{ (}\Omega\text{)}}{L \text{ (cm)}} \]\[= \frac{AR}{L} \text{ }\Omega\text{·cm}\]So ohm-centimeter ((\Omega)·cm) is also a unit of resistivity.
Variation of Resistivity with Temperature
Like resistance, resistivity also varies linearly with the temperature of the material. Suppose \(\rho_1\) is the resistivity of a material at temperature \(T_1\), and \(\rho_ 2\) is the resistivity of the same material at temperature \(T_2\) degrees Celsius. Then,\[\rho_2 = \rho_1[1 + \beta_1(T_2 – T_1)]\]\[\Rightarrow\; \beta_1 = \frac{\rho_2 – \rho_1}{\rho_1(T_2 – T_1)}\cdot\cdot\cdot(1)\]Where \(\beta_1\) is the temperature coefficient of resistivity and obviously it is the same as the temperature coefficient of resistance.
Definition of Temperature Coefficient of Resistivity
We can define the temperature coefficient of resistivity as the change of resistivity per unit resistivity at the initial temperature for a change of per one degree Celsius.
Proof of Equivalence
We can easily prove that the temperature coefficient of resistance equals the temperature coefficient of resistivity at a particular temperature.
Suppose \(R_2\) is the resistance at \(T_2\) degrees Celsius and \(R_1\) is the resistance at \(T_1\) degrees Celsius. Therefore, as per the equation of change of resistance for variation of temperature is \[R_2 = R_1[1 + \alpha_1(T_2 – T_1)]\]Now we can write,\[R_1 = \rho_1 \frac{L}{A} \& R_2 = \rho_2 \frac{L}{A}\]So we can write the above equation as\[\rho_2 \frac{L}{A} = \rho_1 \frac{L}{A}[1 + \alpha_1(T_2 – T_1)]\]This implies\[\rho_2 = \rho_1[1 + \alpha_1(T_2 – T_1)]\]Here,\[\alpha_1 = \frac{\rho_2 – \rho_1}{\rho_1(T_2 – T_1)}\cdot\cdot\cdot(2)\]Comparing equation (1) and (2), we can conclude that the temperature coefficient of resistance equals the temperature coefficient of resistivity.
