Let us discuss the effect of temperature on resistance. When the temperature of a conductor increases, its resistance also increases. This relation is linear. In other words, the change in resistance is directly proportional to the change in temperature.
Mathematical Relationship
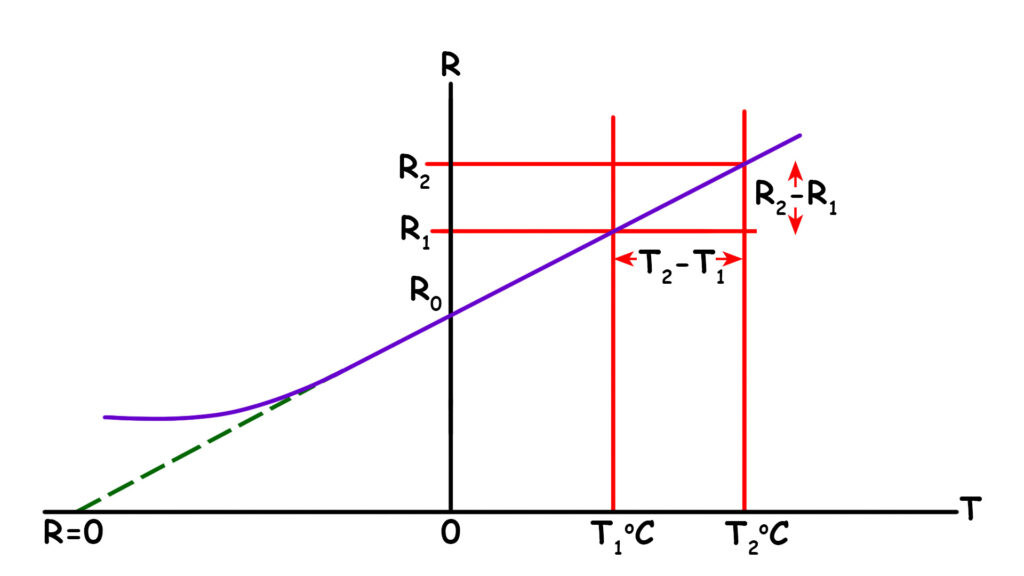
If R1 is the initial resistance of a particular resistor or conductor at T1 °C, and R2 is the resistance at T2 °C, then we can write\[R_2 – R_1 \propto T_2 – T_1\]
Dependence on Initial Resistance
Now, this change in resistance also depends on the initial value of resistance that we have measured at T1 °C.
For example, suppose you have a 10 Ω resistance at 20°C, and it becomes 12 Ω at 30°C. What is the change in resistance? That is 12 – 10 = 2 Ω.
Now consider a 20 Ω resistance at 20°C. Obviously, this will become 24 Ω at 20°C. So in the previous case, the increase in resistance was 2 Ω, but in this case, the change is 4 Ω.
Therefore, the change that occurs in resistance also depends upon the initial value of the resistance. So we can ultimately say that the change in resistance is also directly proportional to the initial resistance. That means,\[R_2 – R_1 \propto R_1\]
Temperature Coefficient of Resistance
So finally, we can write, \[R_2 – R_1 \propto R_1(T_2 – T_1)\]Or\[R_2 – R_1 = \alpha_1 R_1(T_2 – T_1)\]This \(\alpha_1\) is the constant of proportionality. For this relation, we refer to this \(\alpha_1\) as the temperature coefficient of resistance at T1°C. So,\[\alpha_1 = \frac{R_2 – R_1}{R_1(T_2 – T_1)}\]That means \(\alpha_1\) is the fraction by which the initial resistance R1 increases per degree change of temperature (per °C).
Final Resistance Formula
So we can finally write the value of resistance at T2°C as,\[R_2 = R_1[1 + \alpha_1(T_2 – T_1)]\]We should remember that this equation holds good for both rise and fall of temperature.
Behavior of Pure Metals
Take an example of pure metal. In pure metals, we have found that the relation between temperature and resistance is linear. That means the effect of temperature on resistance is linear. Now, when the temperature increases from its initial value, the resistance will also increase. On the other hand, when the temperature decreases, the resistance will also decrease at the same rate.
Theoretical Zero Resistance Point
This means that for decreasing temperature, resistance will continually decrease linearly following the temperature-resistance line. Obviously, this straight line will intersect the horizontal zero axis at a certain point. Since the horizontal axis represents temperature, if we measure this point from zero, we will get a specific temperature. That point indicates that at that temperature, theoretically, the resistance of the conductor will become zero.
Superconductivity Concept
In this way, all metals and other conducting materials will have a particular temperature value at which their resistance becomes theoretically zero. That means the conductor becomes a superconductor. This is the theoretical assumption.
Practical Behavior
However, practically, when the resistance of a conductor becomes very low near that critical temperature, the resistance-temperature line becomes almost parallel to the horizontal temperature axis of the graph. That means after a certain level, a conductor cannot decrease its resistance further, even if the temperature decreases below the critical temperature of the conductor.
Value of Temperature Coefficient of Resistance at Different Temperatures
The value of \(\alpha\) is not constant. Moreover, it is different for different temperatures. We can get a clear idea from the equation we have derived for the temperature coefficient of resistance \(\alpha_1\) at \(T_1\)\[\alpha_1 = \frac{R_2 – R_1}{R_1(T_2 – T_1)}\]So the value of \(\alpha_1\) corresponds to the temperature \(T_1\) and \(R_1\) is the initial resistance that is going to change due to the change in the temperature from \(T_1\).
Temperature Coefficient for Reverse Temperature Change
Now consider if we reduce the temperature from T₂ degrees Celsius to \({T_1}^oC\). In that case, the variation of temperature is also \(T_2 – T_1\), and the change of resistance is also \(R_2 – R_1 \). But here, the initial resistance from where the resistance value starts changing is \(R_2\), not \(R_1\). So the temperature coefficient of resistance will be different from \(\alpha_1\). According to the initial temperature of the conductor, it will be \(\alpha_2\), and the initial resistance in that case is \(R_2\).
Equations for Reverse Temperature Change
Here, in the second case, for changing the temperature from T₂ to \(T_1\), we can write\[R_1 – R_2 = R_2 \alpha_2 (T_1 – T_2)\]Or\[R_1 = R_2[1 + \alpha_2(T_1 – T_2)]\]Now\[\frac{R_1 – R_2}{T_1 – T_2} = R_2 \alpha_2\]Or\[\frac{R_2 – R_1}{T_2 – T_1} = R_2 \alpha_2\]So the slope of the straight line is the product of initial resistance and the temperature coefficient.
From this relation, we can write\[\alpha_1 R_1 = \alpha_2 R_2\]
Final Relationship Between \(\alpha_1\) and \(\alpha_2\)
Now, we know\[R_2 = R_1[1 + \alpha_1(T_2 – T_1)]\]Hence,\[\alpha_2R_2 = \alpha_2R_1[1 + \alpha_1(T_2 – T_1)]\]\[\Rightarrow \alpha_1R_1 = \alpha_2R_1[1 + \alpha_1(T_2 – T_1)]\]\[\Rightarrow \alpha_1 = \alpha_2[1 + \alpha_1(T_2 – T_1)]\]From here, we can write\[\alpha_2 = \frac{\alpha_1}{1 + \alpha_1(T_2 – T_1)}\]This is the relation between Temperature Coefficient of Resistance of different temperatures.
Definition of Temperature Coefficient of Resistance
In view of the dependence of \(\alpha\) on the initial temperature, we may define the temperature coefficient of resistance at a given temperature as the change in resistance per ohm per degree Celsius change in temperature from the given temperature.
Temperature Correction of Resistance
Suppose we have measured the resistance of a conductor at 32°C as 12 Ω. The current rating of that conductor corresponds to 75°C. This means when the conductor carries its rated current, the temperature of that conductor should not rise above 75°C.
We have measured the resistance at 32°C. So we need to determine the resistance value of the conductor at 75°C. This corrected resistance tells us the behavior of the conductor when it will carry its maximum rated current. Therefore, it is essential to know the corrected resistance value.
Generally, most of the standards give the value of the temperature coefficient of resistance at 20°C. Therefore, we need to convert this temperature coefficient for 32°C, because we have measured the resistance at 32°C. Then we have to use the general formula for calculating the actual resistance at 75°C.
From the table of standard values of temperature coefficient, we get,\[\alpha_{20} = 0.00393 \text{ per °C for copper}\]Because in our example, we have considered the material of the conductor is copper.
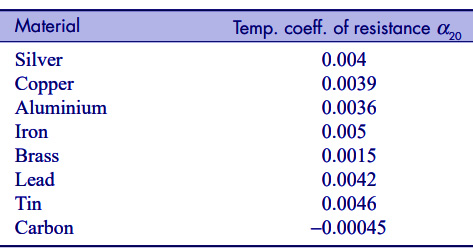
Therefore,\[\alpha_{32} = \frac{\alpha_{20}}{1 + \alpha_{20}(32 – 20)}\]\[= \frac{0.00393}{1 + 0.00393 \times 12}\]\[= 0.00375 \text{ per °C}\]So the correct temperature coefficient at 32°C is \(\alpha_{32} = 0.00375\) per °C.
Now, as per the formula,\[R_{75} = R_{32} \times [1 + \alpha_{32}(75 – 32)]\]Where \(R_{75}\) is the corrected resistance value at 75°C.\[R_{75} = 12 \times [1 + 0.00375 \times 43]\]\[= 13.94 \text{ Ω}\]So the corrected resistance at 75°C is 13.94 Ω.
It is always preferable to correct our resistance measurement for the temperature at the maximum temperature limit of the equipment for better assessment of the behavior of the equipment at full load conditions.
Video on the Effect of Temperature on Resistance
