DSLP Calculator – Detailed with Formulas
Inputs:
- Lightning Mast height \( h \) (m)
- Maximum height to be protected \( h_x \) (m)
- Distance between two Lightning Masts \( S \) (m)
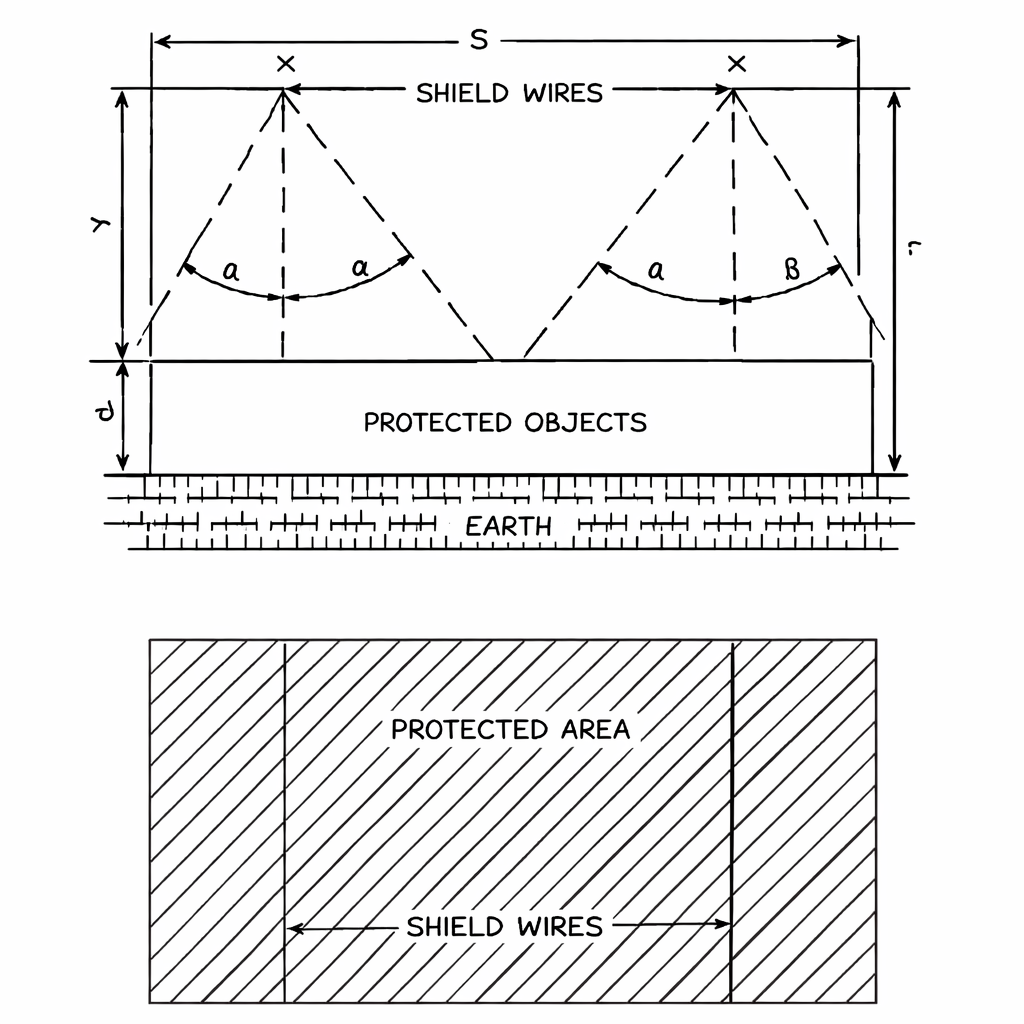
Lightning protection is essential in every high-voltage substation. The lightning masts (LMs) shield equipment from direct strokes. We use the DSLP calculation to check this shielding.
We need three main inputs for this calculation.
- Mast height: \(h\)
- Maximum equipment height to protect: \(h_x\)
- Distance between two masts: \(S\)
Calculate Single Mast Protective Radius
A lightning mast protects a circular zone. Say, \(r_x\) is the radius of this protection zone at height \(h_x\).
We compare the equipment height with two-thirds of the mast height\[h_x \le \frac{2}{3}h\]. This check decides which formula we use.
Lower Equipment (Better Protection)
If \(h_x \le \frac{2}{3}h\), the protective radius is,\[r_x = 1.5h\left(1 – \frac{h_x}{0.8h}\right)\]
Obviously, this formula gives a larger protection radius because the equipment is lower.
Higher Equipment (Reduced Protection)
If \(h_x > \frac{2}{3}h\), the radius becomes\[r_x = 0.75h\left(1 – \frac{h_x}{h}\right)\]
This formula gives a smaller radius because shielding is reduced near the top.
Calculate Maximum Permissible Mast Spacing
Two masts can work together to protect equipment in between. However, they must not be too far apart.
The limit is calculated by\[S_{\max} = 7(h – h_x)\]We define the height difference as: \[h_a = h – h_x\]The spacing condition is simple\[S \le S_{\max}\]If this is true, the two masts provide proper shielding.
Calculate Equivalent Midpoint Height
When two masts stand at a distance S, we imagine a virtual mast at the midpoint. Its effective height is
\[h_o = h – \frac{S}{7}ho\]
This height reduces if the spacing increases. It helps us calculate midspan protection.
Calculate Midspan Protective Distance
We check whether the midpoint can protect equipment at height \(h_x\). We again use the same two-case approach.
\[b_x =\begin{cases}1.5h_o\left(1 – \frac{h_x}{0.8h_o}\right), & h_x \le \frac{2}{3}h_o \\[6pt]0.75h_o\left(1 – \frac{h_x}{h_o}\right), & h_x > \frac{2}{3}h_o\end{cases}\]