What is Skin Effect?

Skin effect is a phenomenon that occurs in conductors carrying alternating current. Actually, when an alternating current flows through a conductor, it tries to flow through the outer layer of the conductor. The central or inner portion of the conductor carries much lower current than the outer surface. As a result, the current distribution across the cross-section of the conductor becomes uneven.

Alternating current flows through the conductor normally at 50 Hertz. This effect increases with increasing supply frequency.

As the alternating current tries to flow through the outer surface, meaning the skin of the conductor, we refer to this phenomenon as skin effect.

Theory

Actually, alternating current produces an alternately changing magnetic field in the conductor. According to Faraday’s law of electromagnetic induction, this changing magnetic field induces eddy currents within the conductor itself. This induced eddy current opposes the main current flowing through the conductor. As the maximum number of magnetic field lines links the central portion, the influence of the alternating magnetic field is maximum here. So the opposition of the induced eddy current is maximum at the center of the conductor.

Although the changing magnetic field also links the outer surface of the conductor, the number of magnetic flux linkages is less than that of the central axis of the conductor. So the induced eddy currents are less at the surface of the conductor. Therefore, the opposition by the eddy currents is also less on the surface of the conductor. So the main current tries to concentrate at the surface of the conductor.

This is the phenomenon of skin effect. Therefore, this phenomenon increases the overall resistance of the conductor. This is because the current now faces a lesser effective cross-sectional area to flow. After all, it has to flow through the area nearer to the surface of the conductor only.

Skin Effect Formula

We use a mathematical formula to determine skin effect. Specifically, the formula for skin effect is\[\delta = \sqrt{\frac{\rho}{\pi f \mu}}\]Here, \(\delta\) represents the skin depth of the conductor. Moreover, it indicates the depth through which significant current flows. We measure \(\delta\) in meters.

Additionally, \(\rho\) denotes the resistivity of the conductor material. We express it in ohm-meters. Furthermore, f represents the frequency. Also, \(\mu\) indicates the magnetic permeability. From this equation, we can observe that when frequency increases, skin depth decreases. Therefore, frequency plays a crucial role in skin effect.

For example, consider a copper conductor at 60 Hz. In this case, the skin depth equals 8.5 mm. However, when frequency rises to one megahertz, skin depth drops to just 0.066 mm. Consequently, this demonstrates how frequency influences this effect.

Diagram

This diagram illustrates the current distribution due to skin effect. Specifically, it shows the current density at different depths from the conductor surface. Moreover, each curve represents a particular frequency. Furthermore, the curves demonstrate changes in current intensity. We can observe sharp changes in current density for curves representing higher frequencies. In contrast, lower frequency curves appear flatter. Therefore, frequency significantly impacts the distribution pattern.

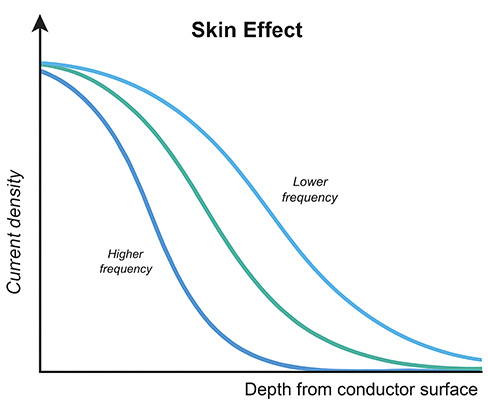
Additionally, the dark red color on the outer surface highlights maximum current density. Specifically, it shows concentration at the outer portion of the conductor’s cross-section. Meanwhile, the center shows lower current density. Hence, the visual representation clearly demonstrates the skin effect phenomenon.

Skin Effect in Transmission Lines

Engineers face tremendous challenges due to skin effect in transmission conductors. Firstly, it increases the effective resistance of the transmission line. Consequently, ohmic power loss increases dramatically. Moreover, this creates significant operational problems.

Similarly, underground transmission lines face the same type of challenges. Specifically, skin effect increases the effective resistance of underground cables. As a result, higher ohmic losses occur. Furthermore, this produces higher heat generation in the conductor. Consequently, this higher heat generation causes derating of the conductor. Therefore, the cable’s current-carrying capacity reduces.

Formula for Transmission Lines

Due to skin effect, the AC resistance and DC resistance of the same conductor differ. Specifically, we apply this ratio when the conductor carries alternating current. The formula is
\[\frac{R_{ac}}{R_{dc}} = 1 + \frac{x^2}{48} + \frac{x^4}{2880} \]Here, x represents the ratio of conductor radius to the skin depth. Moreover, this formula helps engineers to calculate the actual resistance. Thus, they can design systems more accurately.

Skin Effect in Power Systems

Skin effect also influences all electrical equipment connected to the power system. Firstly, it increases the effective resistance of the alternator’s armature, generating the power. Consequently, generator efficiency decreases.

Additionally, this effect increases the effective resistance of transformer windings. As a result, the efficiency of power transformers reduces. Therefore, overall system performance suffers.

Moreover, it reduces the current-carrying capacity of bus bars. Specifically, solid bus bars used in indoor systems experience this problem. However, for outdoor systems, we use different solutions. We use either stranded power conductors or hollow aluminum pipes. Importantly, both of these designs reduce skin effect. Hence, they improve system performance.

Disadvantages of Skin Effect

Due to skin effect, the effective resistance of conductors increases. Thereby, ohmic power loss increases significantly. Therefore, this imposes continuous expenditure on the utility. Indeed, power loss means loss of money. Consequently, operational costs rise substantially.

Additionally, current tries to flow through the conductor’s surface due to skin effect. Meanwhile, the central portion of the conductor remains unused. In other words, valuable conductor material goes unutilized.

Furthermore, concentrated current at the conductor’s surface produces excessive heat. As a result, the insulation becomes degraded faster. Therefore, the lifespan of equipment is reduced. Consequently, maintenance and replacement costs increase.

Finally, as resistance increases due to skin effect, the voltage drop in the transmission line increases. Thus, power quality suffers. Moreover, this affects the entire distribution network. Therefore, voltage regulation becomes poorer.

How to Reduce Skin Effect

Use of Stranded Conductor

We avoid using solid conductors. Instead, we always try to use stranded conductors. Because stranding increases the effective surface portion of the conductor. As a result, the current gets more paths to flow. Therefore, the overall resistance of the conductor reduces. So, this improves current flow efficiency.

Use of Hollow Conductor Pipes

We avoid using solid conductors in substations. Instead, we always try to use hollow aluminum pipes. Specifically, we use them in bays and bus bars. Hollow pipes have nothing in the inner portion. Therefore, we make efficient use of aluminum or copper.

Milliken Conductor

In the Milliken conductor, we not only use stranded conductors. Moreover, we use multiple groups of stranded conductors. Additionally, these groups are insulated from each other. Specifically, thin layers of insulating material separate the groups. Furthermore, this arrangement improves the current distribution through the conductor. As a result, it increases the effective cross-sectional area. Hence, resistance decreases significantly.

Increasing Cross-Sectional Area

We increase the effective cross-sectional area of conductors deliberately. Specifically, we use bundle conductors instead of a single conductor of large diameter. Consequently, this improves overall performance.

Increasing Conductor Spacing

We increase the spacing between two conductors intentionally. Specifically, when we increase conductor spacing, the proximity effect reduces. Moreover, this also reduces the skin effect. Therefore, proper spacing improves conductor efficiency. Hence, power losses decrease substantially.